I saw something in a paper which didn't make much sense to me... Of course it is also possible that I’m
just stupid and overlooking explanations... so I’ll write here what I found and
you can decide on your own.
This is a
table I reproduced from that paper. The reason I don’t simply make a screenshot
of the table in the paper is that I could be false. And in that case I don’t
want to falsely accuse the paper (or its authors) of error.
So I tried
to provide some anonymity to the paper… (for now).
Pre are
measurements taken before... something... and post afterwards (if you didn't guess it).
The same
people were tested in pre and post and the sample size was 21.
What surprised me were the tiny standard deviations for some of the Variable 1 and 2, especially in combination with the range given.
So I tried
to find some numbers that would fulfill the criteria given (mean, standard
deviation and range) for these 4 (or 8) variables. First my "results" for the first four
variables pre:
As you can
see I managed to find values (for each participant) that add up to the given
mean for every variable. (I should note here that the third and the fourth
variable are ratings on a numerical (not visual) rating scale, so values other
than other than X.0 and X.5 might not be so likely.)
I also tried to get the SD as much to the given value as possible. You see what I was able to get.
I also tried to get the SD as much to the given value as possible. You see what I was able to get.
(SD excel
is the SD calculated by excel and SD me is the SD calculated by me with help of
excel, i.e. I set up the formula myself cos I didn’t know what formula excel
was using. I didn’t calculate it by hand though, because there would be no chance
to get a correct result that way.)
The SDs
(dark blue row) I got are much higher than the given SDs for the first two
variables (variable 1 pre and 2 pre).
I don’t
know, obviously there’s a chance that I’m just dumb and didn’t do it correct.
In order to get a lower SDs than those I got, I then replaced these numbers (for 2 to 20) with the mean of the
first and the last value. I can’t change the first and the last value, because
they are given in the table. Obviously, when I do that the mean is not "correct"
anymore, but I should get the
lowest possible SD (min and max value fixed) with that, shouldn't I?
Apparently, for the first two variables the SD is still a lot higher than the given SD. (For the third and fourth variable I was able to get the same (very close, but I could have tried longer) SD as given in the table anyways.)
Apparently, for the first two variables the SD is still a lot higher than the given SD. (For the third and fourth variable I was able to get the same (very close, but I could have tried longer) SD as given in the table anyways.)
In the next
table you can see that this is similar for these variables in post:
Just for
the variables 1 and 2 (pre and post) I couldn’t find any values that met the
criteria.
So I thought maybe the authors inadvertently reported the SEM instead of the SD. Maybe it is possible to call the SEM SD because after all the SEM is a measurement of deviation which is standardized too.
So I thought maybe the authors inadvertently reported the SEM instead of the SD. Maybe it is possible to call the SEM SD because after all the SEM is a measurement of deviation which is standardized too.
Therefore I tried to get the SEM to be the value reported for the SD:
That is
possible for the first to variables (pre and post) but I didn’t manage to do
that for the third and fourth variable.
Maybe they
reported the SEM for Variable 1 and 2 and the SD for Variable 3 and 4. I don’t know. The other possibility is that
I made a mistake, obviously.
Anyways… in
the paper they did t-tests with these variables. So I tried
to do that too… Obviously I don’t know in which order the values were… so
if I just take my fabricated values I get a far off t-value.
Sorry for my SPSS speaking German, but it isn’t important
anyways (as it is obvious that this gives the false t-values):
At least I
saw some significances in that output window for once… :(
And mean,
SD and SEM are about the same as in my Excel calculation.
Fortunately
the paper tells me which t-values I ought to get:
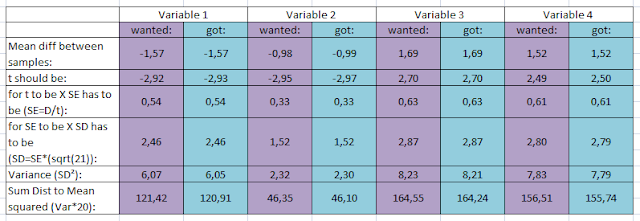
So I
calculated what the Sum of the (distance to the mean)² of the differences
between the two conditions (pre and post) needs to be in order to get
* the
"correct" mean difference between the samples
* and therefore also the "correct" t-value.
Here’s a
table for that:
Then I
tweaked my… why not call them "data" ("data" not: data) to fit these criteria.
Although I
was not able to reproduce exactly these numbers, it went quite well and I got
pretty close.
Obviously there are a lot of solutions, especially if I don't meet the SD-criteria for each Variable as specified in the table (I could have tried for the 3rd and 4th variable, but I didn't).
Here (one possible set of ) the individual "data" I used to get this values:
Obviously there are a lot of solutions, especially if I don't meet the SD-criteria for each Variable as specified in the table (I could have tried for the 3rd and 4th variable, but I didn't).

Here (one possible set of ) the individual "data" I used to get this values:
Btw, I
gained some data-fabrication knowledge doing this (which I had not previously had!! All my
data are honestly p-hacked :( :( [1]).
Want to hire me?
SPSS too thinks that the new t-values are much better:
I know this might seem like a really small point... since the t-values are all possible and hopefully correct. I don't know. It's relevant for effect-size estimation, for example.
I can be false (just to say this again, because maybe I'm not seeing something really obvious).
Another point I noticed is that they report a mean of 0.36 (SD=0.29) in some questionaire data. I can't say anything about this, since I don't know their participants personally, but seriously... I doubt it.
I found this graph which represents the answer-distribution for a non-clinical population for either this scale or a quite similar one (it's not clear to me from the paper; there is a long and a short version):
The reported mean for that scale (out of that other study) is 9.4 with a SD of 7.83). My participants (healthy controls) have a mean value of 12.4 (with min=4, max=19, and SD=3.5). Of course the mean can be lower (then there) in different populations at a different time and if especially people with probably low values in that questionaire are recruited. But 0.36 seems really low to me.
I don't know if they did some transformations on that or whatever, but it is not reported.
Oh, and even though I obviously didn't report a lot of varibles/values from that study I didn't omit a control group... it's just pre and post.
(Again, I don't exclude my stupidity at all. Sorry for the repetition.
I thought very long about whether or not to post this, but I think the SD and the mean of the questionaire are too low...)
I can be false (just to say this again, because maybe I'm not seeing something really obvious).
Another point I noticed is that they report a mean of 0.36 (SD=0.29) in some questionaire data. I can't say anything about this, since I don't know their participants personally, but seriously... I doubt it.
I found this graph which represents the answer-distribution for a non-clinical population for either this scale or a quite similar one (it's not clear to me from the paper; there is a long and a short version):
The reported mean for that scale (out of that other study) is 9.4 with a SD of 7.83). My participants (healthy controls) have a mean value of 12.4 (with min=4, max=19, and SD=3.5). Of course the mean can be lower (then there) in different populations at a different time and if especially people with probably low values in that questionaire are recruited. But 0.36 seems really low to me.
I don't know if they did some transformations on that or whatever, but it is not reported.
Oh, and even though I obviously didn't report a lot of varibles/values from that study I didn't omit a control group... it's just pre and post.
(Again, I don't exclude my stupidity at all. Sorry for the repetition.
I thought very long about whether or not to post this, but I think the SD and the mean of the questionaire are too low...)
[1] Obviously p-hacking is bad
too! I’m well aware of that. I don’t even know what is worse…
edit/addition:
1. I didn't want to imply that the data were fabricated. I don't think so!! The title refers to what I did in this post. I think it wouldn't make much sense if the data (of the SD-variables) were fabricated, because even then they should have an SD that is possible (if I'm right that the one they report is not possible with that mean and range). (And the reported t-value is possible with much higher SDs.)
For the mean on the questionnaire-data I think it is most likely that it is either a mistake, the data were transformed (though that is not mentioned) or the participants were influenced.
And while I'm at it, I think there could be two other possible mistakes in that paper. One is relatively clear (because they report the study protocol in a slightly different order at different points in the paper) and the other it is not certain imo.
2. Christopher at the neurotroph-blog did some R-simulations on the Standard Deviations. You can read his blog-post here.
edit/addition:
1. I didn't want to imply that the data were fabricated. I don't think so!! The title refers to what I did in this post. I think it wouldn't make much sense if the data (of the SD-variables) were fabricated, because even then they should have an SD that is possible (if I'm right that the one they report is not possible with that mean and range). (And the reported t-value is possible with much higher SDs.)
For the mean on the questionnaire-data I think it is most likely that it is either a mistake, the data were transformed (though that is not mentioned) or the participants were influenced.
And while I'm at it, I think there could be two other possible mistakes in that paper. One is relatively clear (because they report the study protocol in a slightly different order at different points in the paper) and the other it is not certain imo.
2. Christopher at the neurotroph-blog did some R-simulations on the Standard Deviations. You can read his blog-post here.














Hmm, interesting... Re: the SDs, I think they must be wrong for Variable 1 and Variable 2. Maybe they are in fact SEMs which were wrongly reported as SDs. Well spotted. That could well be an honest error.
ReplyDeleteFor the questionnaire with mean 0.36 (SD=0.29), this seems odd too. is it possible that the authors are expressing scores as a fraction of the maximum possible score on the scale? (so 1.00 = maximum score)?
Thank you very much for your comment!!
DeleteYes, I didn't want to imply that they deliberately changed the SD! (That wouldn't make much sense.)
Hm, so if the max-score for the questionaire-data was 45 and the participants reached mean 36% of that then that would be a mean score of 16.2.
And if the scale had a max of 60, that would be a mean score of 21.6.
A bit high, but (I think) much more likely than 0.36...
However, I think, unless it is common to report it like that they should say that they expressed their score as a fraction because it changes the interpretation.
Everything I found about these scale(s) just speaks about sum-scores.
Overall I would say that you've uncovered an issue here with the SD/SEM, and the questionnaire means are a question mark too. Whether there is any more serious issue lurking behind it, is another question. You could write to the authors and ask them to clarify. If it's an honest mistake they should put in a correction.
DeleteThe last author is my professor (supervisor).
DeleteS/he thinks the SDs are fine... haven’t shown him/her the excel-stuff, though. I did that just recently/now (and mentioned the SDs a long time ago... and believed/accepted that they were fine then).
So, just to be fair, it is in my interest too not to name the paper... not ONLY because I could be false. But I also was really unsure (i.a. because others think the SDs are fine).
It’s complicated.
Hmmm... that's a tricky situation. In that case I would say that the relevant question is, is this an isolated case? Or are there similar problems in many papers?
ReplyDeleteI don’t know. I mainly read only the papers that are relevant for me... (probably I should read more... but I know how they are produced, which reduces the motivation to read them...). (The one from my post is very/the most relevant for me.)
Delete(However, there is likely a (much) bigger mistake in another paper. But I only know about it from a colleague and I can’t prove or show it, because for that it would be necessary to have the data. I don’t know much about it, so I don’t know if it is correct mention this.
Another thing (but not a mistake) is, my professor lied at a congress. S/he said the data weren’t unblinded yet (but which group was probably which according to the data & his/her opinion), when in fact they were (and s/he knew it very well but doesn’t like the results)).
But I’m thinking, what is the difference to (a lot of) p-hacking...? Probably all the fraudsters had the same thought.... Probably my prof thought the same thing before lying.... Hm.... :(